Ejemplos de derivadas, es de una función según la capacidad de velocidad con la que puede cambiar su valor.
Es de una función calculada la velocidad y su límite tomando en cuenta un intervalo tal como lo considera la matemática, mientras que en física determina siempre dentro de un cambio la cuantía sobre una determinada magnitud.
Ejemplos de derivadas, cociente incremental

Cociente incremental es la variación de crecimiento de “y” con respecto a la variación de crecimiento con respecto a “x”
Ay/h = f (xo + h) – f /xo)/ h
Ejemplos de derivadas, interpretación geométrica en un punto
El cociente incremental:
Tg oc = Ay/h = f (Xo + h) – f (Xo)/h
Geométricamente la pendiente de la cuerda determinada por los puntos de la gráfica de la función en Xo y X + h
Tg oc = Ay/h
Si se deja fijo Xo se achica tanto como se quiera, se obtiene una sucesión de rectas secantes que pasan por “a” y como el cociente incremental determina la pendiente de la cuerda, si aplicamos el limite de ese incremento, obtenemos la derivada que es la pendiente de la recta tangente a la curva de dicho punto.
Por ejemplo:
f’ (2) = 4— es la recta tg a la curva en Xo = 2”
f(x) = 2x xo = 1
f(x) = 1/2×2 – 1 Xo = 2
f(x) = 3 Xo = 1
f(x) = x2 Xo =1
f(x) = x3 Xo =1
f (x) = 1/x Xo =1
f (x) = raíz cuadrada de x Xo =9
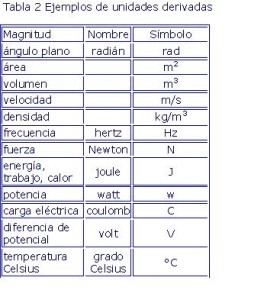
Ejemplos de derivadas, tablas
1) y = f (x) = k—y = f’ (x) =0
2) y = f (x) =x — y’ =f’ () =1
3) y = f(x) = x—y’ = f’ (x) = h’ (x) + g’ (x)
4) y = f (x). g (x) — y’ = f’ (x). g (x) + f (x). g’ (x)
5) y = f(x) / g (x) — y’ = f’ (x). g (x) – f (x). g’ (x)
6) y =xn — y’ = n . Xn-1
7) y = In x — y’ =1/x
8) y = loga x — y’ = loga e/x
9) y = ex — y’ =ex
10) y = sen x — y’ = cos x
11) y = cos x — y’ = sen x
12) y = tg x — y’ = 1/ cos2 x
13) y = — y’ = ax In a x’

Ejemplos de derivadas, Ejercicios
Dado:
a) f(x) = (x3 – In x + e2x)2
b) f (x) =3 sen2 2x
c) f (x) = cos2 (2x + pi)
d) f (x) = raíz cuadrada de 2×3 + e-x + 2x
f) f (x) = In (cos x)
Respuestas:
a) =2
b) = 25 x4
c) = 3 x3
d) = 3×5
f) = 0,4x
Contínua
Una función será derivable con una condición contínua y cuyos incrementos pequeños de los elementos de dominio ejercen incrementos pequeños en el valor de la función.
Las variaciones serán cada vez más pequeñas con incrementos del mismo tipo hasta aproximarse al límite cero. Lee ejemplos de fracciones equivalentes.
[…] En realidad dado que cada número entero es un conjunto, dos números son iguales si y solo si tienen los mismos elementos o serán iguales si y solo si los representantes que los definen son elementos equivalentes. Lee: ejemplos de derivadas. […]