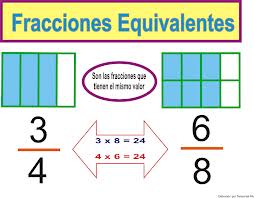
Ejemplos de fracciones equivalentes

Ejemplos de fracciones equivalentes si bien a simple vista parecen distintas siempre cuentan con un valor igual.

Son iguales porque al multiplicar o dividir el numerador o denominador por un número igual mantendrá el valor.

Siempre debes multiplicar o dividir por el mismo número tanto el numerador como el denominador.

Ejemplos de fracciones equivalentes, multiplicando

Si tienes ½, éste es igual a 2/4 y a 4/8 al multiplicar el numerador y el denominador de estas fracciones por 2, por ello son equivalentes.

Ejemplos de fracciones equivalentes, dividiendo

En el caso de la división de fracciones comenzando por la de mayor valor si tienes 18/36 y 6/12 te dará como resultado ½. Divides 17/36 por 3 lo cual es igual a 6/12. Recuerda que el numerador y el denominador lo estarás dividendo por 3, por ello 18/36 es igual a 6/12. Continúas dividiendo numerador y denominador siempre por el mismo número realizando una simplificación, entonces dividirás por 6 y obtendrás ½ como resultado final.

Ejemplos de fracciones equivalentes, simplificando

Puedes continuar la división hasta el máximo posible simplificando la fracción para obtener una simple.

Recuerda también que siempre debe tratarse de números enteros tanto en el numerador como en el denominador para poder multiplicar o dividir ambos a la vez. No se tratará de una equivalente si sumas o restas cualquier numero al numerador o denominador.

Obtendrás una equivalente cuando por el mismo número multiplicas o divides el numerador y el denominador.

Ejemplos de fracciones equivalentes, amplificando

Tal como has realizado una simplificación, inversamente puedes realizar una amplificación, en este caso multiplicando el numerador y el denominador por el mismo número.

Por ejemplo puedes obtener dos equivalentes si partes de por ejemplo 2/3 y lo multiplicas por 6, entonces obtendrás que 2/3 es igual a 12/18.

Ejemplos de fracciones equivalentes, comprobando

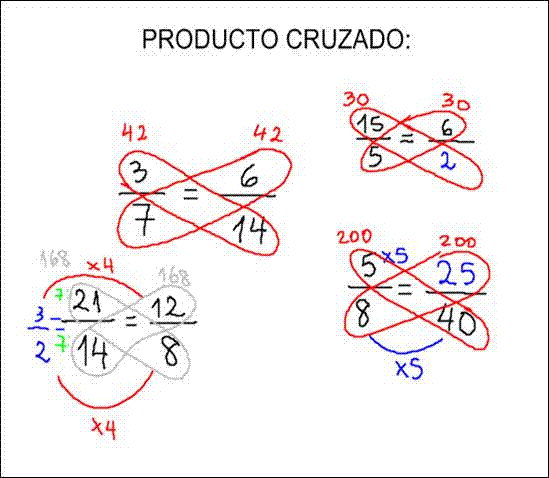
Puedes comprobar de forma fácil si has realizado una operación correcta, multiplicando el numerador de la primera por el denominador de la segunda y viceversa. Por lo tanto habías obtenido 2/3 igual a 12/18, entonces multiplicarás 2 x 18 y 3 x 12. Ambas multiplicaciones te darán por resultado 36, lo cual te indica que has realizado una operación correcta.

Ejemplos de fracciones equivalentes, representando

Toda fracción es representada por un numerador y un denominador separados entre ellos con una línea que los divide ½, uno es el numerador y 2 es el denominador.

Mientras el denominador está representando la cantidad en iguales partes en que es posible fraccionar una unidad, el numerador está representando el entero.

También pueden ser representadas gráficamente, por lo general con figuras geométricas, rectángulos o círculos divididos de acuerdo a la cantidad de partes que representa a fracción. Toda la figura representa la unidad y será divida en la cantidad de partes que indique el denominador colorando las partes indicadas por el numerador.

Por ejemplo ¾ será representado gráficamente con tres partes coloradas de las cuatro que representan el entero.

Ejemplos de fracciones equivalentes, clasificación

Se clasifican según la relación existente considerando el numerador y el denominador.

Entonces puedes encontrarte con una impropia donde el número mayor corresponderá al numerador, por ejemplo 8/2, 9/4 etc.

Una propia mostrará el número del denominador mayor al numerador, por ejemplo ½, 3/8,5/9, etc.

Una reducible se trata de una fracción en la que puede simplificarse con un numerador y denominador con números no primos.

Una irreducible, se trata de una en la que tanto el numerador como el denominador cuentan con números primos y no tienes posibilidad de simplificarla.

Una entera o aparente es aquella en se encuentra representando a cualquier número entero, por ejemplo 5/5, 7/7, 2/2 etc.

Una inversa la obtendrás de otra invirtiendo numerador y denominador, por ejemplo 2/4 y 4/2. Continúa leyendo en ejemplos de algoritmos.